首页 计算机科学 算法

# 排序算法

# 时间复杂度O(n2)O(n^2) 级排序算法

# 冒泡排序

核心思想

像冒泡一样，两两比较，每次找出最大值 / 最小值，一般有三种写法：

  • 写法一：一边比较，一边两两交换，将最大或者最小冒到最后
  • 写法二：优化写法一，使用一个变量记录当前轮次是否发生过交换，如果没有发生交换，表示已经有序，直接结束
  • 写法三：优化写法二，在写法二的基础上记录上一次发生交换的位置，下一轮排序到该位置时就停止比较

# 代码实现 - 方法一

def bubble_sort(arr):
    for i in range(len(arr)-1):
        for j in range(len(arr)-1-i):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 代码实现 - 方法二

def bubble_sort(arr):
    # 添加 tag 记录是否发生替换
    tag = True
    for i in range(len(arr)-1):
        if tag is False:
            break
        tag = False
        for j in range(len(arr)-1-i):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                tag = True
    return arr

# 代码实现 - 方法三

有些复杂，暂时先不记

# 选择排序

核心思想

双重循环数组，每一轮比较，找到最小元素的下标并交换至首位

# 代码实现

def select_sort(arr):
    for i in range(len(arr)):
        minIndex = i
        for j in range(i+1, len(arr)):
            if arr[j] < arr[minIndex]:
                minIndex = j
        arr[i], arr[minIndex] = arr[minIndex], arr[i]
    return arr

# Tips

排序算法的稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r [i] = r [j]，且 r [i] 在 r [j] 之前，而在排序后的序列中，r [i] 仍在 r [j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

冒泡排序是稳定的，选择排序是不稳定的

实际意义：当要排序的内容是一个对象的多个属性，且原本的顺序存在意义，在二次排序后需要保持先前的顺序

# 插入排序

核心思想

插入排序可以形象的类比成打扑克牌，从左向右，每次将一个元素插入其左侧合适的位置，有两种写法，交换法和移动法

# 代码实现 - 交换法

def insert_sort(arr):
    for i in range(len(arr)):
        j = i
        while j >= 1 and arr[j] < arr[j-1]:
            arr[j], arr[j-1] = arr[j-1], arr[j]
    return arr

# 代码实现 - 移动法（减少插入的次数）

def insert_sort(arr):
    for i in range(1, len(arr)):
        curr_num = arr[i]
        j = i - 1
        while j >= 0 and arr[i] < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = curr_num

# 时间复杂度O(nlogn)O(nlogn) 级排序算法

# 希尔排序（非常依赖增量序列的好坏）

核心思想

希尔排序在插入排序的基础上进一步优化，克服了插入排序每次只交换两个相邻元素的不足，基本步骤如下：

  • 将待排序数组按照一定间隔分为多个子数组，每组分别进行插入排序，这里的间隔分组不是取连续的一段数组，而是每次跳跃一定间隔取一个值构成一组
  • 逐渐缩小间隔进行下一轮排序
  • 最后当间隔为 1 时，直接使用插入排序，因为之前的操作使得数组已经基本有序了，最后只需要进行少量的交换就能完成任务

# 代码实现 -(每组内采用插入排序移动法)

def shell_sort(arr):
    gap = len(arr) // 2
    while gap > 0:
        # Grouping
        for group_start_index in range(gap):
            # Insertion Sort
	        for current_index in range(group_start_index + gap, len(arr), gap):
            	current_number = arr[current_index]
                pre_index = current_index - gap
                while pre_index >= group_start_index and current_number < arr[pre_index]:
                    # Shift positions backward
                    arr[pre_index + gap] = arr[pre_index]
                    pre_index -= gap
                # current_number found its position and sits down
                arr[pre_index + gap] = current_number
        gap //= 2

# 时间复杂度分析

希尔排序时间复杂度较难分析，平均复杂度界于O(n)O(n) 到O(n2)O(n^2)，普遍认为最好是O(n1.3)O(n^{1.3})。

为什么希尔排序可以比O(n2)O(n^2) 更好？排序算法本质上是消除逆序对的过程，对于随机数组，逆序对数量是O(n2)O(n^2)，冒泡、插入、选择都只能通过「交换相邻元素」的方式，需要进行O(n2)O(n^2) 次，而希尔排序通过交换距离较远的元素，使得一次交换能消除一个以上的逆序对。

# 堆排序

核心思想

这里的第一个 while 循环构造堆，其中 sink () 方法通过下沉的方式对 a [1] 到 a [n] 的元素进行排序，之后第二个 while 循环将最大的元素 a [1] 和 a [n] 交换并缩小堆的容量，直至堆变为空。

# 时间复杂度分析

堆排序优势：最坏情况下也能达到 O (nlogn) 的时间复杂度

堆排序的不足：

但现代系统的许多应用 很少使用它，因为它无法利用缓存。数组元素很少和相邻的其他元素进行比较，因此缓存未命中的次 数要远远高于大多数比较都在相邻元素间进行的算法，如快速排序、归并排序，甚至是希尔排序。

# 代码实现 - 堆排序

def heap_sort(arr):
    n = len(arr)
    k = n // 2
    while k >= 1:
        sink(arr, k, n)
        k -= 1
    while n > 1:
        # exch(a, 1, n)
        arr[1], arr[n] = arr[n], arr[1]
        n -= 1
        sink(arr, 1, n)

# 代码实现 - 由上至下的堆有序化（下沉）的实现

# 下沉代码，先比较当前节点的左右孩子谁更大，之后将大的孩子和当前节点比较，如果当前节点更大直接退出，否则交换当前节点和大的孩子节点
def sink(arr, k, n):
    # 这里用 2*k 是因为第一个元素下标是从 1 开始的，那么他的左孩子就是 2*k
    while 2*k <= n:
        j = 2*k 
        if j < n and arr[j] < arr[j+1]:
            j += 1
        if not arr[k] < arr[j]:
            break
        arr[k], arr[j] = arr[j], arr[k]
        k = j

# LC 练习

  • # 215. 数组中的第 K 个最大元素

    思路：用堆排序，维护一个长度为 k+1 的数组（小顶堆），每次新来一个元素，比较和堆顶元素的大小，如果小于堆顶元素就 continue，否则和堆顶元素替换并执行下沉（sink）操作，初次构建堆的时间复杂度为O(k)O(k)， 算法第四版 P206 命题R：用下沉操作由 N 个元素构造堆只需少于 2N 次比较以及少于 N 次交换 ，之后每来一个元素执行一次比较和 sink 操作，比较时间复杂度为O(n)O(n)，sink 为O(logk)O(logk)，总共时间复杂度为O(nlogk)O(nlogk)。

    nums = [3,2,1,5,6,4]
    k = 2
    class Heapq:
        def __init__(self, arr):
            self.arr = arr
            self.heap_sort(self.arr)
        
        def sink(arr, k, n):
            # 这里用 2*k 是因为第一个元素下标是从 1 开始的，那么他的左孩子就是 2*k
            while 2*k <= n:
                j = 2*k 
                if j < n and arr[j] < arr[j+1]:
                    j += 1
                if not arr[k] < arr[j]:
                    break
                arr[k], arr[j] = arr[j], arr[k]
                k = j
        def build_heap(self.arr):
            n = len(self.arr)-1
            k = n // 2
            while k >= 1:
                self.sink(arr, k, n)
                k -= 1
            
       	def insert(num):
            if num <= self.arr[1]:
                return
            else:
                self.arr[1] = num
                n = len(self.arr)-1
                self.sink(self.arr, 1, n)
    class Solution:
        def findKthLargest(self, nums: List[int], k: int) -> int:
            if len(nums) < k:
                return max(nums)
            arr = [0]
            arr.extend(nums[:k])
            heap = MyHeapq(arr)
            for num in nums[k:]:
                heap.insert(num)
    • 备注：如果要时间复杂度严格保持在 O (n)，需要使用快速选择排序
  • # 剑指 Offer 40. 最小的 k 个数
    思路：同样采用堆排序，最后输出堆中元素，时间复杂度为O(nlogk)O(nlogk)。
    class MyHead:
        def __init__(self, arr):
            self.arr = arr
            self.leng = len(self.arr) - 1
            self.build_heap(self.arr, self.leng)
        def sink(self, arr, k, n):
            while k <= n:  # 这里改成 k 改成 2*j，后面的第二个 if 判断就不需要 j<=n 这个条件
                j = 2 * k
                if j < n and arr[j] < arr[j+1]:
                    j += 1
                if j <= n and arr[k] < arr[j]:
                    arr[k], arr[j] = arr[j], arr[k]
                k = j
        def build_heap(self, arr, n):
            k = n // 2 + 1  # 从最后一个非叶子结点开始遍历 
            while k >= 1:
                self.sink(arr, k, n)
                k -= 1
        def insert(self, num):
            if num < self.arr[1]:
                self.arr[1] = num
                self.sink(self.arr, 1, self.leng)
            else:
                pass
        def print(self):
            return self.arr[1:]
    class Solution:
        def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
            new_arr = [0]
            new_arr.extend(arr[:k])
            myhead = MyHead(new_arr)
            for num in arr[k:]:
                myhead.insert(num)
            return myhead.print()
# 快速排序
核心思想：利用了分治思想
  • 首先选择一个基数；
  • 遍历数组，将基数小的放到左边，将基数大的放到右边；
  • 之后将左右两个区域再看成自赎罪，重复上述步骤
（如何从逆序对的角度思考，好像不好从这个角度出发）
# 代码正确，但是 leetocde 卡时间
def quicksort(arr, start, end):
    if start >= end:
        return
    middle = partition(arr, start, end)
    quicksort(arr, start, middle-1)
    quicksort(arr, middle+1, end)
def partition(arr, start, end):
    pivot = arr[start]
    left = start+1
    right = end
    while left < right:
        if arr[left] <= pivot:
            left += 1
        else:
            arr[left], arr[right] = arr[right], arr[left]
            right -= 1
    if arr[left] <= pivot:
        arr[left], arr[start] = arr[start], arr[left]
        return left
    else:
        arr[left-1], arr[start] = arr[start], arr[left-1]
        return left-1
# 换成左右指针同时移动的代码，减少不必要的交换次数
def partition(arr, start, end):
    left = start+1
    right = end
    pivot = arr[start]
    while True:
        while arr[left] < pivot:
            if left == end:
                break
            left += 1
        while arr[right] > pivot:
            right -= 1
        if left >= right:
            break
        arr[left], arr[right] = arr[right], arr[left]
    arr[start], arr[right] = arr[right], arr[start]
    return right
分析时间复杂度：平均时间复杂度为O(nlogn)O(nlogn)，但在数组有序的情况下会退化为O(n2)O(n^2)，这是因为每一次遍历划分的左半部分都是空的，也就失去了分治的效果，下一次还要进行 n-1 次比较。
# 归并排序
核心思想：如果有两个已经有序的子数组再得到最终有序的数组只需要O(n)O(n) 的时间复杂度就可以，那么怎么得到有序的子数组呢？通过二分的方式，长度为 8 的数组可以通过两个长度为 4 的数组得到，长度为 4 的数组可以通过两个长度为 2 的数组得到，依次类推。
# 代码实现 - 基础版本
# 将两个有序数组合并
def merge(arr1, arr2):
    result = []
    i, j = 0, 0
    while i < len(arr1) and j < len(arr2):
        if arr1[i] <= arr2[j]:
            result.append(arr1[i])
            i += 1
        else:
            result.append(arr2[j])
            j += 1
    while i < len(arr1):
        result.append(arr1[i])
        i += 1
    while j < len(arr2):
        result.append(arr2[j])
        j += 1
    return result
def merge_sort(arr, start, end):
    if start == end:
        return [arr[start]]
    middle = (start + end) // 2
    left = merge_sort(arr, start, middle)
    right = merge_sort(arr, middle+1, end)
    return merge(left, right)
# 代码实现 - 减少临时空间的开辟
# 将两个有序数组合并
def merge(arr, start, end, result):
    middle = (start + end) // 2
    # 数组 1 首尾位置
    start1 = start
    end1 = middle
    # 数组 2 首尾位置
    start2 = middle+1
    end2 = end
    # 三个数组开始位置
    i, j, k = start1, start2, start1
    while i <= end1 and j <= end2:
        if arr[i] <= arr[j]:
            result[k] = arr[i]
            i += 1
            k += 1
        else:
            result[k] = arr[j]
            j += 1
            k += 1
    while i <= end1:
        result[k] = arr[i]
        i += 1
        k += 1
    while j <= end2:
        result[k] = arr[j]
        j += 1
        k += 1
    # 记得要返回回去
    for i in range(start, end+1):
        arr[i] = result[i]
def merge_sort(arr, start, end, result):
    if start == end:
        return
    middle = (start + end) // 2
    merge_sort(arr, start, middle, result)
    merge_sort(arr, middle+1, end, result)
    return merge(arr, start, end, result)
时间复杂度分析：时间复杂度为O(nlogn)O(nlogn)，空间复杂度为O(n)O(n)。
为什么一般用快排而不是归并排序？
# 时间复杂度O(n)O(n) 级排序算法
# 计数排序
核心思想：计数排序不是通过比较的方式，而是通过数字自身的属性进行排序，编写代码时首先需要一个大小为O(n+k)O(n+k) 的辅助数组 counting，counting [i] 表示比数字 i 小的数字个数之和，之后将原数组的每个值映射到 result 数组上，result 的下标和该下标对应的值都是原数组的值。最后将 result 数组复制到原数组中。时间复杂度为O(n+k)O(n+k)，这里 n 指的是数组长度，k 指的是数据的范围大小。
# 代码实现
class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        if len(nums) < 2:
            return nums
        max_num = nums[0]
        min_num = nums[0]
        for num in nums:
            if num < min_num:
                min_num = num
            elif num > max_num:
                max_num = num
        leng = max(max_num - min_num + 1, len(nums))
        counting = [0] * leng
        for num in nums:
            counting[num-min_num] += 1
        pre_count = 0
        for i in range(leng):
            pre_count += counting[i]
            counting[i] = pre_count - counting[i]
        result = [0] * leng
        # result 保存下标位置到值的映射关系，最后排序是默认按照下标位置来的
        for num in nums:
            result[counting[num-min_num]] = num
            counting[num-min_num] += 1
        for i in range(len(nums)):
            nums[i] = result[i]
        return nums
# LC 练习
# 1122. 数组的相对排序
思路：两种做法，第一种自定义比较函数，第二种计数排序，对于 python 来说，用元组来进行比较，首先定义一个哈希表 rank，保存(arr2[num],index)(arr_2[num],index)，如果元素 x 出现在哈希表中，就使用二元组 (0, rank (x))，如果不出现就采用(arr1[i],0)(arr_1[i],0).
# 思路一
class Solution:
    def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
        rank = {}
        for index, num in enumerate(arr2):
            rank[num] = index
        def cmp(a):
            return (0, rank[i]) if a in rank else (1, a)
        arr1 = sorted(arr1, key=cmp)
        return arr1
时间复杂度
# 思路二
因为数字范围不大，所以可以采用计数排序方法
class Solution:
    def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
        freq = {}
        max_num, min_num = max(arr1), min(arr1)
        new_arr = [0] * len(arr1)
        for num in arr1:
            freq.setdefault(num, 0)
            freq[num] += 1
        index = 0
        for num in arr2:
            for i in range(freq[num]):
                new_arr[index] = num
                index += 1
            freq[num] = 0
        for i in range(min_num, max_num+1):
            if i not in freq:
                continue
            for _ in range(freq[i]):
                new_arr[index] = i
                index += 1
        return new_arr
# 基数排序
核心思路：基数排序也是一种非比较型的排序算法，思想是按照数字的每一位进行排序，首先需要将所有数字统一长度，之后从最低位开始排序，这里排序通常使用计数排序（在每一轮排序时需要保证稳定性），因为取值范围在 0～9，时间复杂度为O(d∗(k+N))O(d*(k+N))，其中 N 为数字个数，k 表示每个基数的取值范围，d 为最大数字位数，空间复杂度为 O (n+k)。详细步骤如下图所示：
img
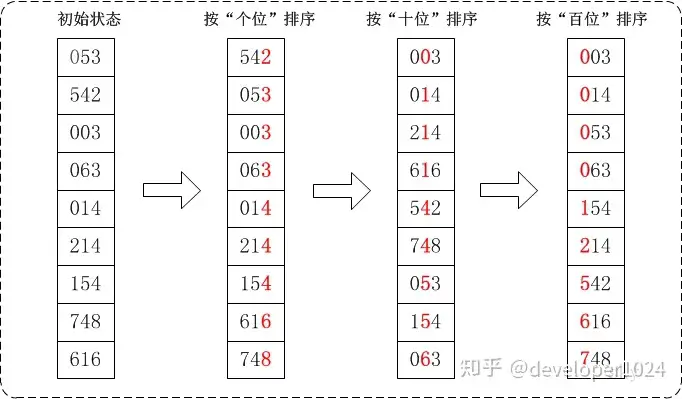
# 代码实现
def radix_sort(arr):
    if len(arr) == 0:
        return
    max_num = max(arr)
    max_length = 0
    while max_num != 0:
        max_length += 1
        max_num /= 10
    counting = [0] * 10
    result = [0] * len(arr)
    dev = 1
    for i in range(max_length):
        for value in arr:
            radix = value // dev % 10
            counting[radix] += 1
        pre_count = 0
        for i in range(10):
            pre_count += counting[i]
            counting[i] = pre_count - counting[i]
        for value in arr:
            radix = value // dev % 10
            result[counting[radix]] = value
            counting[radix] += 1
        for i in range(len(arr)):
            arr[i] = result[i]
        counting = [0] * 10
        dev *= 10
参考：
排序算法
算法 第四版
排序算法之基数排序
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
Barton 微信支付
微信支付
Barton 支付宝
支付宝
Barton 贝宝
贝宝