<meta name="referrer" content="no-referrer" />
# 本文问题定义
本文定义问题如下:给定起点、终点,出发时间和一个旅行时间限制,本文的任务是在旅行时间限制内获得一个热门度很高的路线。
# 本文主要想法
发现热门路径是非常重要的,同时热门路径会随着时间变化而发生变化的。先前有关搜索热门路线的工作没有考虑到路线的热门度会随着时间变化而变化(其实 13 年 sigmod 论文已经考虑到了时间的影响,用户需要输入一个时间段,通过这个时间段在线构建 footmark 图,因此在线的时间开销较大,同时时间段设置的很大)
# 本文贡献:
- 定义一个 TDHP 问题去找到具有时间依赖和旅行时间限制的热门路径
- 提出了一个构造热门度函数的方法
- 提出了一个新的搜索策略去找到 TDHP,并使用优化的方法加速这个过程
- 实验评估 effectiveness and efficiency
# 热门度函数定义
在这篇文章当中,为了减少计算边的热度所带来的开销,提出了一个 TimeParti 算法将连续热度函数进行离散化。
时间戳集合:

假定时间被划分为,那么边在该时段的热门度定义如上(这里感觉不太合理,原文说是 timestamp set, 但这里 记录的应该是在 中所有经过的轨迹数量而不是轨迹到达时间 t 的集合,如果很多轨迹都在同一时刻达到,但是只记录了时间戳,那么热门度就相应的会下降)
时间区间离散化:rhis

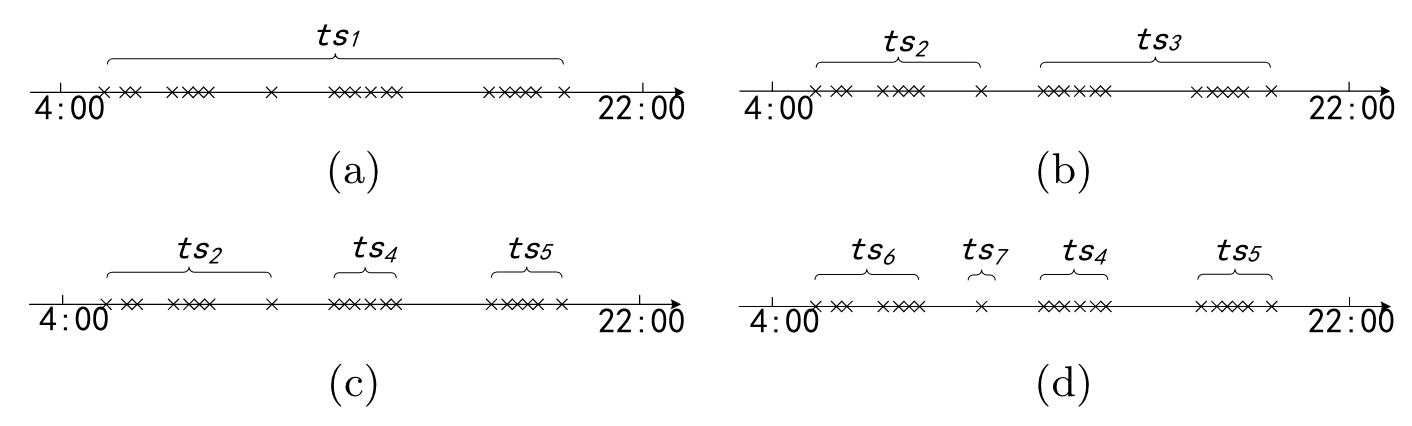
这里采用的方法是二分 K-means,设定一个阈值,判断每一个 SSE 是否会超过阈值,下图为划分示意图(这里若多条轨迹都在时刻 t 到达,应该认为只有一个 t)

# 在线搜索算法
本文拓展了 A * 算法,传统的 A * 算法是去找权值最短的结点,本文是去找热门度最高的结点,算法流程如下:

# 剪枝策略
# 利用时间限制进行剪枝
考虑到时间限制的因素,假定扩展到顶点 u,这时再顶点 u 已经超过了限制时间,则该结点被剪枝。对于启发式函数 h (x) 来说,边同样可以用类似的方法进行剪枝。

# 热度函数过滤
对于边,每条边都有一个最早到达时间和最晚到达时间,即不早于一个时间段到 i,不晚于一个时间段离开 j(这里为什么不设置每个点都有一个最早到达时间和最晚到达时间:h (x) 统计的是边的权重)

疑问:
1、需要用户输入时间限制信息,会给用户带来一定的麻烦
2、没有考虑到终点的影响,只是单纯的统计一段时间内轨迹经过的数量,这样对于一些终点会受到误判
3、对于上图第三行 FT 的时间复杂度的计算感觉不清楚
可借鉴的地方:
1、划分时间的方式